数学摇滚 

音乐本是旋律的艺术，摇滚的诞生也多是叛逆的情绪产物，但一切皆有可能，后摇中的一部分，开始打破节拍常规，在歌曲和音乐中交错换拍，于是诞生了实验室产物一般，科幻的数学摇滚，在你不经意中它可能偷偷又多加了几个音符，即使你数对前面再多拍子它都随时可能戛然而止。

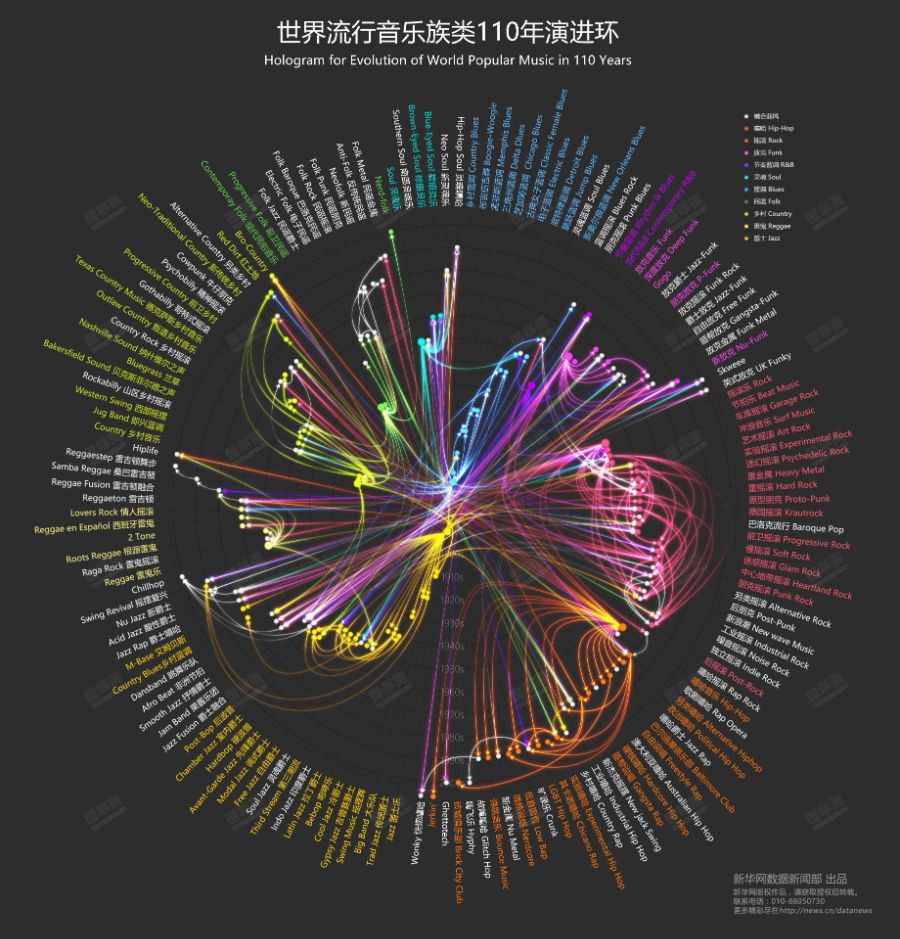
充满理科色彩的音乐，想想就觉得叛逆。

数学，这个让人头疼的学问，还能被人做成摇滚了？

确实如此。

讲起数学摇滚，很多人的第一反应都是和实验摇滚有关、近乎偏执的靡靡之音。没错，数学摇滚（Math Rock）的确是属于一种实验摇滚。它80年代源于美国，风靡世界各地，特别是日本。也是因为它听上去比较复杂，如数学运算，故此称为“数学摇滚”。

数学摇滚曲风大多混合：噪音摇滚（Noise rock)、后摇滚(Post rock)、前卫摇滚(progressive rock)、简约音乐(Minimal music)、电子音乐(Electronic music)等。

它的一个特点是编曲复杂，经常使用不规则停顿或开始；不自然节拍结构（odd time signatures）、棱形旋律（Angular melody）、对位法（counterpoint）、延伸和弦（extended chords）、不协调和弦（dissonant chords）、非典型和弦进行(atypical Chord progression）
一般摇滚乐都以 4/4 拍 作歌曲结构，而数学摇滚则频繁使用不对称节拍。如 7/8 拍, 11/8 拍, 13/8 拍，并于歌曲中交错换拍，例如一小段 9/8 拍，转换至 8/8 拍 ，再转换至 6/8 拍，让听众有错摸的诡异感觉。又例如，在同一首乐曲，不同的乐器，使用 3/4 拍的鼓、4/4 拍的吉他、3/4 拍的贝斯；却让每样乐器巧妙地于“不同音轨”上“对在一起”，听起来又顺畅不碍耳。接触过后摇滚（Post Rock）的人乍一听，可能觉得数学摇滚听起来很像后摇滚，但是实际上数学摇滚要比后摇滚更明快、更复杂，那么它的特点是什么呢？

数学摇滚最大的特点就是节奏更复杂，很容易从架子鼓中听出来。它显得浓厚而复杂，同时充满着艰涩的拍子记号和缠结在一起的乐段。（也许不断变换的节拍会让听歌的你露出一脸懵逼的表情..？）

数学摇滚的旋律经常是很短的一些动机组成的，而不是很长很连贯的主旋律。因此很多数学摇滚和后摇一样，也没有主唱，吉他也没有独奏（Solo）段。主要都是吉他的反复乐段（Riff）来构成乐曲。总体上它更倾向于情感的抒发，听上去会更像情绪摇滚（Emo Rock）很多倾向于创意与技巧的表现，听上去更实验；甚至还有些会融合爵士的色彩…

但是数学摇滚的反复乐段又和普通的摇滚不一样；很多摇滚喜欢直接扫和弦，但是数学摇滚的反复乐段是一个简短的旋律；很多摇滚是单个吉他演奏的反复乐段，但是数学摇滚喜欢用多个声部演奏。和弦是通过几个吉他和贝斯同时演奏旋律来产生的，类似于古典音乐的对位（Counterpoint），因此出现的和弦会丰富许多。而且由于吉他便于演奏弯音、滑音等，旋律可能会有更加丰富的音响效果。

数学摇滚经常以多个乐器同时演奏不同节奏的反复乐段的方式编曲，叫做复节奏（Polyrhythm），这点可能比较相似于极简主义（Minimalism）音乐；因为这些乐器经常重复相同的短旋律，所以会形成一种复杂的节奏偏移的奇妙感觉。很多数学摇滚是用音色非常干净的清音吉他演奏的，鼓也经常是比较清脆的，使得每个乐器都能听得十分清晰。

当然也有数学摇滚乐队是用低度过载或失真吉他的，还有用金属鼓的演奏法。也有乐队大量采用合成器，让音色更加丰富。数摇的复杂，燃烧的是编曲人的大脑，完整的作品不但非常流畅，且节奏感超强。

                                       文策划部蔡颖

                                    图新华网